Главная / Системы счисления
Системы счисления
Системы счисления – это знаковые системы, обеспечивающие запись чисел по установленным приёмам (правилам) с помощью принятых в этих системах символов, которые называются цифрами.
Или немного короче: система счисления – это совокупность правил записи чисел с помощью цифр.
Для написания чисел и выполнения математических операций с ними обычно используется десятичная система счисления. Ее название объясняется тем, что в основе этой системы лежит основание 10 (десять). Это означает, что в десятичной системе счисления любое число выражается упорядоченной последовательностью десяти различных цифр: 0, 1, 2, 3, …. 9.
Однако, применяют не только десятичную, но и другие системы счисления, например восьмеричную, шестнадцатеричную и т.д. Так, например, в компьютерах для хранения и преобразования чисел применяется не десятичная, а двоичная система счисления, то есть система счисления с основанием 2. В этой системе любое число записывается с помощью двух цифр: 0 и 1, и поэтому такое число называется двоичным числом. Примеры двоичных чисел: 000; 001; 010011.
Существует два больших класса систем счисления: позиционные и непозиционные. В позиционных системах счисления значение любой цифры зависит от места (позиции), которое эта цифра занимает при записи конкретного числа. К непозиционным системам счисления можно отнести, например, римскую систему счисления, в которой для записи чисел используются буквы латинского алфавита: I (1), V (5), X (10), L (50), C (100), D (500), M (1000). Количество цифр, которое можно использовать для записи любого числа в позиционной системе счисления называется основанием этой системы счисления. Основание системы счисления указывает также на то, во сколько раз отличаются значения одинаковых цифр, находящихся в соседних позициях числа.
Рассмотрим любое десятичное число, например триста двадцать два (322). Это число состоит из суммы трех сотен, двух десятков и трех единиц:
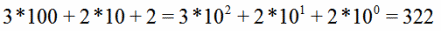
В этом числе в двух соседних разрядах записаны одинаковые цифры (2), значения которых (2 и 20) отличаются между собой в десять раз.
101000111.
Двоичная система счисления
Выбор двоичной системы счисления для хранения чисел в компьютерах связан, прежде всего, с удобством технической реализации устройств памяти. Запись двоичного числа является более громоздкой, чем десятичного, но для хранения двоичного числа в компьютерах требуются более простые элементы, которые обладают всего двумя устойчивыми состояниями.
В самых первых компьютерах такие элементы были построены на электронных лампах, позже – на транзисторах, а потом вместо транзисторов стали применять микросхемы. На магнитных дисках переключающимися элементами являются элементарные области намагниченности.
Запоминающие элементы в микросхеме или области намагниченности на магнитном диске называются ячейками памяти. Ячейка памяти состоит из разрядов. Количество разрядов соответствует количеству переключающихся элементов в этой ячейке. То есть, для физической реализации каждого разряда используется один переключающийся элемент. В каждом разряде хранится 0 или 1. С помощью одного разряда в двоичной системе можно закодировать два значения: 0 и 1. Ниже представлена таблица, в которой показано, какое максимальное число в двоичной системе счисления можно представить с помощью одного, двух и трех разрядов.
| Деся тичное число |
1 разряд для хранения числа |
2 разряда для хранения числа |
3 разряда для хранения числа |
| 0 |
0 |
00 |
00 |
| 1 |
1 |
01 |
01 |
| 2 |
10 |
10 | |
| 3 |
11 |
11 | |
| 4 |
100 | ||
| 5 |
101 | ||
| 6 |
110 | ||
| 7 |
111 |
Из приведенной таблицы видно, что в двух разрядах можно хранить уже вдвое больше различных значений. В трех разрядах количество этих значений опять удваивается. Таким образом, видно, что существует определенная закономерность. Она заключается в том, что добавление одного разряда для представления двоичного числа увеличивает количество возможных значений, представляемых в этих разрядах вдвое.
Важное достоинство двоичной системы счисления – удобство физического представления цифр и чисел. Недостатком двоичной системы является то, что для записи больших чисел в этой системе требуется довольно много цифр 0 и 1. Это затрудняет восприятие двоичных чисел человеком. Поэтому двоичную систему счисления применяют только для «внутренних нужд» компьютера, а человек, который работает с компьютером, имеет дело с обычными числами, представленными в десятичной системе счисления. Компьютер самостоятельно преобразует вводимые человеком числа в двоичную систему счисления, а результаты вычислений представляет опять в десятичной системе счисления.
Арифметические операции в двоичной системе счисления выполняются по тем же правилам, что и в десятичной или любой другой позиционной системе счисления.
Арифметические действия в двоичной системе счисления
Сложение двоичных чиселПравила выполнения операции сложения чисел в двоичной системе счисления представлены в ниже:
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 (два)
Если при сложении двух цифр значение в каком-либо разряде становится равным или больше основания, то возникает единица переноса в следующий разряд, а в данном разряде записывается нуль. Пример:
11
+
01
Результат 100
При сложении трех единиц в данном разряде записывается единица, а 1 переносится в следующий разряд.
Точно также это правило справедливо и в десятичной системе счисления (если сумма двух цифр в десятичной системе счисления становится равной или больше основания (10), то возникает единица переноса в следующий разряд, а в данном разряде записывается цифра младшего разряда числа, полученного в результате сложения. Например:
17
+
16
Результат 33
В приведенном примере при сложении (7 + 6 = 13) возникает единица переноса в старший разряд, а в данный (текущий) разряд записывается цифра из младшего разряда результата сложения, то есть 3.
Таким образом, в любой системе счисления будет справедливо следующее правило: если при сложении двух чисел в любой системе счисления сумма двух цифр очередного разряда равна основанию системы счисления или превышает его, то в текущий разряд записывают младший разряд этой суммы, а в следующий разряд переносят разницу между текущим значением суммы и цифрой младшего разряда этой суммы.
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
10 – 1 = 1
При двоичном вычитании в том случае, когда разность цифр становится меньше нуля, осуществляется заем из соседней левой цифры уменьшаемого, а нулевое значение данного разряда считается равным 2.
Например:
10111
-
01110
Результат 01001,
или
1001001
-
0011111
Результат 0101010.
То есть, арифметические действия в двоичной системе выполняются по тем же правилам, что и в десятичной системе, но с учетом основания системы счисления.
Сложение – важнейшая операция над двоичными числами в компьютерах. Другие операции – вычитание, умножение, деление – осуществляются в компьютерах обычно с помощью операции сложения.